Michael Sklarz and Norm Miller | August 22, 2016
It is becoming common when ordering appraisals on new loans or refinance applications to also include an AVM (automated valuation model) as these are relatively inexpensive ways to quickly audit value estimates. Aside from concerns over bias in traditional valuation based on most appraisals matching or exceeding the purchase price, value uncertainty should be another concern. Value error is conspicuously absent from traditional appraisals and is a critical component of risk analysis not yet being utilized in the market.
Property values are uncertain for a variety of reasons including but not limited to heterogeneity of the neighborhood making comparison difficult, rapidly changing prices or market conditions, or atypical property not in conformance with the neighborhood. Here we demonstrate that such information can be utilized by adjusting the LTV towards an estimate of value not based the most probable average price but one that takes into account a higher than average proportion of the distribution of possible values. In other words, we can answer the question what is the LTV based on how confident you wish to be about market value?
Statistically, market values are derived to seek the most probable price as of a given date. But the dispersion of prices varies significantly by neighborhood. Below in Exhibit 1, we provide two examples of such price dispersion. Neighborhood A is characterized by a large degree of price dispersion from having multiple developments occur over many years, while neighborhood B is characterized by a neighborhood built out by one developer over two years.
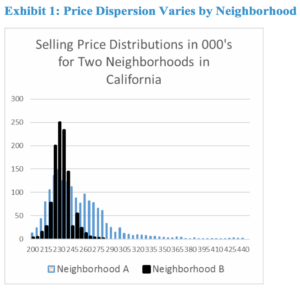
In both neighborhoods above the most probable price for the average home would be similar. But, if we choose to use any confidence level above 50%, this takes into account the uncertainty reflected by the price dispersion. AVMs provide a forecast standard deviation that can be used for exactly this purpose. The standard deviation of the estimate is related to the frequency and quality (degree of similarity) of information available at the time on comparable property. Here we assume a normal distribution, and if a lender wanted to be, for example, just 60% confident that the LTV was the correct maximum we would subtract .842 standard deviations from the most probable price. In this case, instead of using $200,000 as the subject property value when standard deviations run 10% of price, we would use $183,160 and the max loan for a 60% confident max 80% LTV would be $146,528 instead of $160,000. This methodology can be repeated for any level of confidence but the point is that we should not simply use the most probable price as the value since this negates the benefits of adding information about value uncertainty.
Neighborhoods where values are easy to estimate will have low standard deviations and would not be that affected, but neighborhoods that are characterized by heterogeneity and uncertainty would be affected. Additionally, when market conditions are changing or prices are turning the standard deviations of value estimates increase and this would also induce a lender to adjust the loan size to reflect a more confident result.
Conclusion: Equal LTVs are NOT Equal Risk
What we have learned from the last housing downturn is that standardized LTV based lending without regard to the certainty behind the values allows a false sense of security. The reality is that a 90% LTV in a homogeneous and stable neighborhood may be lower risk than an 80% LTV in an area of high price volatility and or uncertainty. The use of standard LTVs while ignoring the risk related information available on value estimates seems imprudent and irresponsible. It is not difficult to incorporate a modest increase in the confidence level from the 50% expected most probable value now provided by appraisals to something just a touch higher. Even moving to 60% confidence would greatly enhance risk analysis and allow for more prudent risk management. For an expanded discussion on the topic, click here.
Download a PDF of this research paper here.
View the original article here.
